Noi viviamo in un mondo di tre dimensioni, in uno spazio tridimensionale. Ogni oggetto solido può essere misurato nelle direzioni nord-sud, est-ovest e infine dal basso in alto.Le figure geometriche nello spazio a tre dimensioni sono studiate dalla geometria solida. Se limitiamo la nostra attenzione a solo due dimensioni abbiamo la geometria piana: la geometria delle figure disegnate su un piano.Possiamo limitarci ancora a considerare le figure dello spazio ad una dimensione, che possono disporsi su una linea retta.E' utile considerare la riflessione degli specchi in ciascuno di questi spazi.

Cominciamo dal più semplice: Linelandia, lo spazio che consiste nei punti d'una retta infinitamente estesa. Immaginate, così per divertimento, che questa retta sia abitata da una razza di creature primitive. I maschi sono segmenti con un occhio formato da un punto in un estremo. Gli occhi non si sviluppano finchè essi non sono adulti. I bambini sono solamente corti segmenti senza occhio.

Per rendere loro la vita più interessante su Linelandia potremmo dotarli di un mondo, consistente in un intreccio di linee,su cui essi possono muoversi avanti e indietro spostandosi come treni sulla rete ferroviaria, ma questo sarebbe eccessivamente complicato, così li confiniamo su una sola retta.

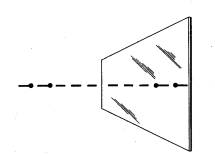
Se mettiamo uno specchio perpendicolarmente ad una di queste rette otteniamo un'immagine riflessa degli abitanti. La figura mostra l'intero piano dello specchio, ma teniamo presente che per gli abitanti di Linelandia lo specchio si riduce a un solo punto sulla loro retta. Notate che i bambini sono esattamente uguali alle loro immagini.

I matematici dicono: il bambino è sovrapponibile alla sua immagine. Significa che noi possiamo immaginare di traslare il bambino lungo la retta fino alla sua immagine, senza farlo ruotare nel piano, cioè senza doverlo girare, fino a farlo coincidere punto per punto con il suo gemello riflesso. Quando questo è possibile diciamo che la figura è simmetrica.

Gli adulti di Linelandia sono simmetrici? No, perché non possono essere traslati sulla retta fino a farli sovrapporre con la loro immagine speculare. Questo perché gli estremi degli adulti sono diversi. Se un adulto ha l'occhio verso est la sua immagine lo ha ad ovest. Naturalmente noi possiamo ruotarlo e farlo coincidere punto per punto con la sua immagine; ma per farlo dobbiamo toglierlo dalla retta e portarlo in un altro insieme: lo spazio a due dimensioni.Poiché un abitante adulto di Linelandia non può essere sovrapposto alla sua immagine, senza entrare in un altro spazio, diciamo che la sua forma è asimmetrica.

C'è un altro modo per distinguere tra simmetria e asimmetria in Linelandia. Se una figura è simmetrica, c'è sempre un solo punto, esattamente al centro della figura, che divide la figura stessa in due metà identiche, una l'immagine dell'altra. Un tale punto è chiamato centro di simmetria.Se poniamo uno specchio in questo punto, perpendicolarmente alla retta, la metà scoperta della figura, insieme alla sua immagine riflessa, riproducono l'intera figura originaria.Un abitante di Linelandia con un occhio in ciascun estremo sarebbe simmetrico? Sì. Questa figura sarebbe sovrapponibile alla sua immagine e avrebbe un centro di simmetria che la divide in due parti uguali.

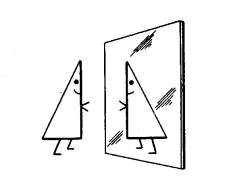
In Flatlandia, lo spazio a due dimensioni della geometria piana, le cose cominciano ad essere più interessanti. Osserviamo la figura : è stilizzato un abitante asimmetrico di Flatlandia e la sua immagine in uno specchio verticale. (Lo specchio è disegnato in tre dimensioni, ma per quel che riguarda l'abitante di Flatlandia esso si riduce ad una linea retta di fronte).Non c'è modo di sovrapporlo alla sua immagine; in nessun modo possiamo traslarlo e farlo coincidere punto per punto con essa.

Se potessimo prenderlo come un pupazzetto di carta, potremmo girarlo e farlo sovrapporre alla sua immagine. Ma questa operazione lo porterebbe in uno spazio a tre dimensioni, e questo non può accadere nel mondo a due dimensioni di Flatlandia.

E' facile disegnare figure piane simmetriche, che cioè non vengono capovolte dello specchio. Quadrati, ellissi, cerchi, triangoli equilateri, triangoli isosceli, stelle, ed i semi delle carte (cuori, quadri, fiori, picche) non cambiano se riflessi.

In Linelandia per una figura simmetrica c'è un punto, il centro di simmetria, che la divide in due metà speculari. In Flatlandia tutte le figure simmetriche possono essere divise in due da una retta chiamata asse di simmetria.

Nel mondo delle tre dimensioni, come in quello a una e due dimensioni tutte le figure possono essere divise in due gruppi: quelle simmetriche e quelle asimmetriche. Le figure solide simmetriche sono quelle che possono essere sovrapposte punto per punto alla loro immagine speculare, con le figure asimmetriche questo non è possibile.Le figure simmetriche nello spazio ad una dimensione hanno un punto di simmetria, quelle simmetriche nello spazio a due dimensioni

hanno assi di simmetria; come ci si può aspettare, le figure simmetriche nello spazio a tre dimensioni hanno piani di simmetria.

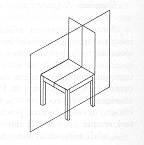
Un cilindro retto, una sigaretta per esempio, ha infiniti piani di simmetria che passano per il suo asse, più un altro piano che taglia l’ asse ad angolo retto. Un cono di gelato ha anche esso infiniti piani di simmetria passanti per il suo asse ma non ha un piano di simmetria ortogonale all’ asse. Un corpo solido, per essere simmetrico, basta che abbia almeno un piano di simmetria. Le piramidi d’Egitto hanno quattro piani di simmetria; un mattone ne ha tre; un tavolo rettangolare ne ha due; una sedia ed una tazzina da caffè ne hanno solo uno.

Immaginate la tazzina tagliata lungo il suo piano di simmetria: se la ponete davanti ad uno specchio vedrete la tazzina intera (questo è dovuto al fatto che l’avete tagliata lungo il suo piano di simmetria). Il fatto che la tazzina abbia un piano di simmetria permette lo scherzo sulle tazzine con il manico a destra o a sinistra.

Lo spazio-tempo della relatività generale viene spesso indicato con il termine misterioso cronotopo ad indicare le sue quattro dimensioni (3 spaziali + 1 temporale). Tuttavia nonostante tale termine abbia un ben preciso significato matematico, la sua visualizzazione presenta dei problemi per il semplice motivo che lo spazio in cui viviamo possiede soltanto tre dimensioni. Le difficoltà e le sensazioni di esseri viventi in spazi con diverse dimensioni è stato genialmente affrontato in un romanzo, scritto nel 1884, dal reverendo E. Abbot dal titolo Flatlandia. Scritto per gli allievi del reverendo al fine di riconciliarli con lo studio della geometria, esso descrive il mondo e le esperienze di esseri confinati in due sole dimensioni. Così descrive il proprio mondo il protagonista (un quadrato):

· · immaginate un vasto foglio di carta su cui delle linee rette, dei triangoli, dei quadrati, dei pentagoni e degli esagoni e altre figure geometriche, invece di restare ferme al loro posto, si muovano qua e là, liberamente, sulla superficie o dentro di essa ma senza potersene sollevare e senza potervisi immergere, come delle ombre, insomma [...] consistenti però, e dai contorni luminosi. Così facendo avrete un idea abbastanza corretta del mio paese e dei miei compagni. Ahimè, ancora qualche anno fa avrei detto (del mio Universo), ma ora la mia mente si è aperta a più alta visione delle cose.

A un certo punto il quadrato entra in contatto con un alieno proveniente da un'altra dimensione, la terza, di cui egli ignorava l'esistenza e di cui i dotti del suo mondo negavano persino la possibilità. L'irruzione dell'essere tridimensionale nel mondo di Flatlandia è un suggestivo esempio di cosa potrebbe accadere se un essere vivente in un'altra dimensione decidesse di irrompere nel nostro mondo tridimensionale. Nel racconto, l'essere tridimensionale tenta di convincere della sua esistenza il riottoso quadrato spostandosi verticalmente, quindi in una dimensione spaziale lui sconosciuta. Il quadrato così racconta la sconvolgente esperienza:

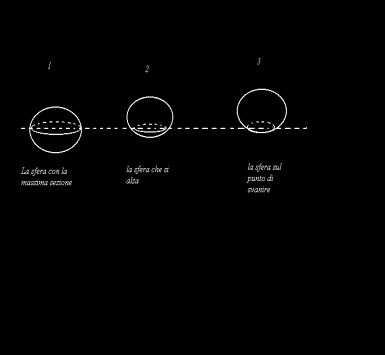
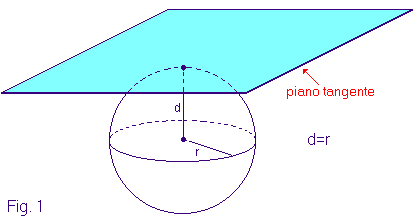
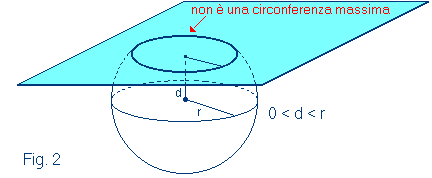
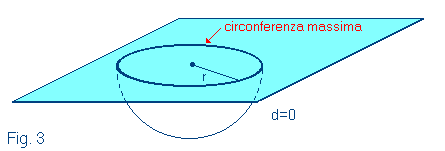
[...] Il rozzo disegno qui esposto mostrerà chiaramente ad ogni bambino della Spacelandia che la Sfera (l'intruso tridimensionale), passando, nel suo moto ascensionale, per le tre posizioni colà indicate doveva per forza manifestarsi a me, o qualunque altro abitante della Flatlandia, sottoforma di Circolo, prima grande, poi piccolo e per ultimo piccolissimo, quasi della misura di un Punto. Ma, sebbene avessi i fatti davanti a me, le cause mi erano più oscure che mai. Tutto quanto potei afferrare fu che il Circolo era diventato più piccolo e che finalmente era svanito, e che adesso era ricomparso e stava rapidamente facendosi più grosso.